Is that real? well yes.
There are a number of mathematical curves that produced heart shapes, some of which are illustrated below.
The first curve is a rotated cardioid (whose name means "heart-shaped") given by the polar equation
 | (1) |
The second is obtained by taking the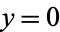 
cross section of the heart surface and relabeling the 
-coordinates as 
, giving the order-6 algebraic equation
cross section of the heart surface and relabeling the 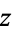-coordinates as 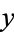, giving the order-6 algebraic equation | (2) |
The third curve is given by the parametric equations
 |  |  | (3) |
 |  |  | (4) |
where ![t in [-1,1]](http://mathworld.wolfram.com/images/equations/HeartCurve/Inline10.gif)
(H. Dascanio, pers. comm., June 21, 2003). The fourth curve is given by
(H. Dascanio, pers. comm., June 21, 2003). The fourth curve is given by![x^2+[y-(2(x^2+|x|-6))/(3(x^2+|x|+2))]^2=36](http://mathworld.wolfram.com/images/equations/HeartCurve/NumberedEquation3.gif) | (5) |
(P. Kuriscak, pers. comm., Feb. 12, 2006). Each half of this heart curve is a portion of an algebraic curve of order 6. And the fifth curve is the polar curve
You might also like,
1 comments:
Copyright violation from original source.
Post a Comment