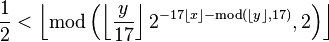Tupper's self-referential formula is a self-referential formula defined by Jeff Tupper that, when graphed in two dimensions, can visually reproduce the formula itself. It is used in various math and computer science courses as an exercise in graphing formulae.
The formula was first published in his 2001 SIGGRAPH paper that discusses methods related to the GrafEq formula-graphing program he developed.
The formula is an inequality defined by:

 

If one graphs the set of points (x,y-k) with and such that they satisfy the inequality given above, the resulting graph looks like this:



This formula itself is a general purpose method of decoding a bitmap stored in the constant k, so it could actually be used to draw any other image. When applied to the unbounded positive range , the formula tiles a vertical swath of the plane with a pattern that contains all possible 17 pixel tall bitmaps. (from: wikipedia)

The cannabis curve, weed, stonerweed leaf, marijuanna, equation, graph, how to

pizza, pic, math, formula, how pizza name is made funny

You need to learn to do this without a calculator. You are not going to be carrying a calculator around with you everywhere you go - 4th grade math teacher

Standard Model Lagrangian (density)

Batman graph equation

where is batman?

bat man in ms excel

You might also like,

• The Love Formula : How to Draw a Heart Shaped Curvy Graph

As Dehaene explains:

Chinese number words are remarkably brief. Most of them can be uttered in less than one-quarter of a second (for instance, 4 is 'si' and 7 'qi') Their English equivalents—"four," "seven"—are longer: pronouncing them takes about one-third of a second. The memory gap between English and Chinese apparently is entirely due to this difference in length. In languages as diverse as Welsh, Arabic, Chinese, English and Hebrew, there is a reproducible correlation between the time required to pronounce numbers in a given language and the memory span of its speakers. In this domain, the prize for efficacy goes to the Cantonese dialect of Chinese, whose brevity grants residents of Hong Kong a rocketing memory span of about 10 digits.

It turns out that there is also a big difference in how number-naming systems in Western and Asian languages are constructed. In English, we say fourteen, sixteen, seventeen, eighteen and nineteen, so one would think that we would also say one-teen, two-teen, and three-teen. But we don't. We make up a different form: eleven, twelve, thirteen, and fifteen. Similarly, we have forty, and sixty, which sound like what they are. But we also say fifty and thirty and twenty, which sort of sound what they are but not really. And, for that matter, for numbers above twenty, we put the "decade" first and the unit number second: twenty-one, twenty-two. For the teens, though, we do it the other way around. We put the decade second and the unit number first: fourteen, seventeen, eighteen. The number system in English is highly irregular. Not so in China, Japan and Korea. They have a logical counting system. Eleven is ten one. Twelve is ten two. Twenty-four is two ten four, and so on.

That difference means that Asian children learn to count much faster. Four year old Chinese children can count, on average, up to forty. American children, at that age, can only count to fifteen, and don't reach forty until they're five: by the age of five, in other words, American children are already a year behind their Asian counterparts in the most fundamental of math skills.

The regularity of their number systems also means that Asian children can perform basic functions—like addition—far more easily. Ask an English seven-year-old to add thirty-seven plus twenty two, in her head, and she has to convert the words to numbers (37 + 22). Only then can she do the math: 2 plus 7 is nine and 30 and 20 is 50, which makes 59. Ask an Asian child to add three-tens-seven and two tens-two, and then the necessary equation is right there, embedded in the sentence. No number translation is necessary: It's five-tens nine.

They can hold more numbers in their head, and do calculations faster, and the way fractions are expressed in their language corresponds exactly to the way a fraction actually is—and maybe that makes them a little more likely to enjoy math, and maybe because they enjoy math a little more they try a little harder and take more math classes and are more willing to do their homework, and on and on, in a kind of virtuous circle. When it comes to math, in other words, Asians have built-in advantage. And also Asians are more willing to try harder than other students.


Read the full story here: Rice Paddies and Math Tests